Stack Building
딥러닝 기초 본문
1. 신경망 개념
인간의 뉴런 체계를 모사
1-1. 인간의 뇌와 신경망
(1) 인간 뇌의 특징

- 1000억 개의 뉴런과 각 뉴런을 연결하는 100조 개의 시냅스의 결합체
- 뉴런은 기본적인 정보처리 단위
- 정보는 신경망 전체에 동시에 저장되고 처리
- 학습에 따라 ‘오답으로 이끄는 뉴런들 사이의 연결은 약화되고, ‘정답’으로 이끄는 연결은 강화
(2) 신경망Neural Network
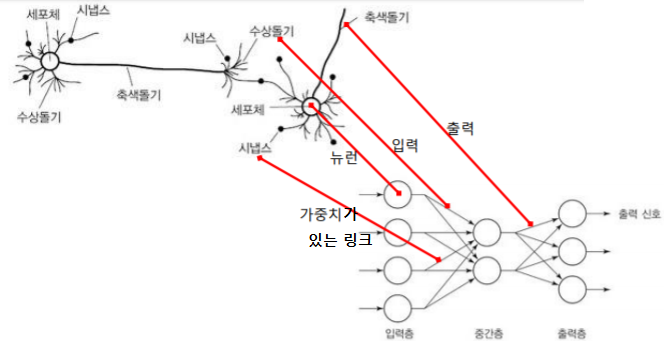
- 인간 뇌를 기반으로 한 추론 모델
- 인간 뇌의 적응성을 활용하여 ‘학습 능력’을 구현함
- 신경망은 뉴런이라는 아주 단순하지만 내부적으로 매우 복합하게 연결된 프로세스들로 이루어져 있음
- 뉴런은 가중치 있는 링크들로 연결
(3) 기계학습과 신경망

기계학습이란 인간이 가지고 있는 학습 능력을 로봇이나 컴퓨터에서 실현하는 기술로 인공지능 분야에서 수학적인 기초가 잘 잡혀있는 분야이다. 신경망은 인간의 신경체계를 모사한 기계 학습의 한 분야이다.
1-2. 신경망의 구조
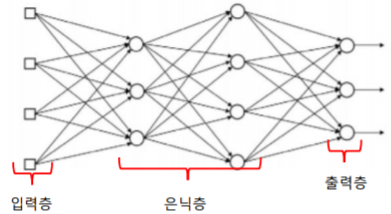
- 입력층: 들어온 신호를 그대로 다음 노드에 전달하는 창구 역할만 수행
- 은닉층: 입력층과 출력층 사이에서 신호의 강도를 조절
- 출력층: 최종 결과를 산출하는 역할
1-3. 신경망의 계층 구조

- 단측 신경망: 입력층-출력층으로 구성된 신경망
- 다층 신경망: 입력층-은닉층(들)-출력층으로 구성된 신경망
- 심층 신경망: 은닉층이 두 개 이상인 다층 신경망
1-4. 신경망의 신호 전달

인간의 뇌는 시냅스를 통해 신호를 조절한다. 신경망에서는 뉴런이 링크로 연결되어 있으며, 각 링크에는 그와 연관된 수치적인 가중치가 있다. 가중치는 장기기억을 위한 기본적인 수단으로, 각 뉴런의 입력 강도, 즉 중요도를 표현한다.
1-5. 신경망과 정보 분류
(1) 정보 분류의 단계

① 신호의 가중치 합 계산
② 가중치 합의 활성함수 값 계산
(2) 활성 함수

활성 함수는 뉴런이 전달받은 신호의 특성을 반영하여 분류 결과를 산출한다. 계단/부호/시그모이드/선형 등의 여러가지 함수가 활성 함수로 적용될 수 있다.
(3) 분류 종류

- 이진 분류: 입력 데이터를 2 개의 범주로 분류. 출력 노드는 1개
ex. 스팸 메일의 판별(스팸 또는 정상), 대출 승인(승인 또는 거절)
- 다범주 분류: 입력 데이터를 n 개의 범주로 분류. 출력 노드는 n개
ex. 동물 분류(사자, 고양이, 호랑이), 색상 분류(빨강, 녹색, 파랑)
2. 단층신경망의 학습 원리
"신경망의 최적 가중치를 자동으로 알아내는 과정에 대하여"
신경망의 뉴런들이 어떤 가중치를 갖느냐에 따라 결과는 크게 달라진다. 그래서 신경망을 학습한다는 것은 최적의 가중치를 자동으로 찾는 문제를 의미한다.
2-1. 신경망의 기본 학습 과정

(1) 가설 설정
- 신경망의 모든 가중치를 적당한 값으로 랜덤 설정
(2) 비용 계산
- 학습 데이터의 각 특징 값을 신경망에 입력해 출력 값을 계산
- 계산된 출력 값과 해당 입력 데이터의 정답을 비교해 오차를 계산
(3) 가설 검증 및 수정
- 계산된 오차를 기준으로 가중치 조절
- (또는) 최소의 오차인지를 판단하한 후 계산된 오차만큼 가중치를 조절
* 비용 계산과 가설 수정 방법은 여러가지가 있다.
2-2. 단층 신경망 학습 과정
(1) 기본 아이디어
"전달받은 신호 값의 크기에 따라 그만큼 오차에 기여한다"

연결 가중치는 입력 노드의 출력과 오차에 비례하여 조절하면 된다. 먼저 오차를 계산하고 오차와 입력 뉴런값을 곱해 가중치를 조절하는 방식이다.
(2) 기본 방법

가설 검증을 위한 비용 계산 방법은 선형 회귀에서 사용했던 평균제곱오차방식을 여전히 사용한다. 그 후 가중치를 수정하고 최적의 가중치를 결정한다. 일반적인 가중치와 오차의 관계는 오목함수 형태를 띤다. 오차를 기준으로 가중치를 변경하고 경사하강법을 이용하여 최적의 가중치를 결정한다.
(3) 향상된 방법

정답과 가설의 오차를 기준으로 가중치를 수정하는 단계에서 활성함수가 시그모이드 함수일때 큰 문제가 발생할 수 있다. 일반적인 가중치와 비용 관계가 (2)의 그림처럼 오목한 데 비해, 시그모이드 함수가 적용된 가설의 가중치와 비용 관계는 울퉁불퉁하여 최적의 비용을 계산하기 어렵기 때문이다. 이 울퉁불퉁한 모양을 매끈하게 오목 함수처럼 만들어주는 방법으로 고안된 것이 교차 엔트로피 함수를 사용하는 방법이다. 두 개의 그래프를 결합하는 것이다. 시그모이드 함수로 분류된 결과의 혼잡도(엔트로피)를 구하여 분류 정확도를 판단하는 방법이다.
2-3. 단층 신경망의 한계


선형 분리 가능 문제에만 적용될 수 있다. 선형 분리 가능 문제는 영역을 구분 짓는 직선을 쉽게 찾을 수 있는 것을 말한다. 선형 분리가 불가능한 문제를 풀기 위해 다층 신경망이 개발되었다.
2-4. 텐서플로우로 단층신경망 시스템 구성
"행렬연산 적용하여 논리곱 연산에 대한 단층신경망 시스템 구성"

논리곱: 입력된 신호가 모두 같을 때 참(1)을 결과로 산출하는 논리 연산
위 그림과 같은 진리표를 학습 데이터로 주고자 하므로, x1, x2는 입력특징값이고 y는 정답임을 알 수 있다. 특징 개수가 2개이므로 입력 뉴런이 2개, 이진 분류이므로 출력 뉴런은 1개만 있으면 된다. 플레이스홀더를 준비하고 가설에 필요한 가중치와 bias(직선의 y절편과 같이 활성함수를 이동시키는 역할)를 설정한 뒤, 가중치의 합과 활성함수를 정의한다. 신경망의 가설 검증과 수정 과정은 선형 회귀와 같다. 전체적인 플로우를 도식화하면 아래와 같다.

아래는 특징의 개수가 많아질 수 있으니 행렬을 이용하여 구조를 단순화한 방식으로 전환한 것이다. 행렬 x에는 특징, 행렬 w에는 가중치를 표현하여 행렬의 곱과 덧셈으로 가중치합을 쉽게 구한다.
- 텐서플로우와 학습 데이터 준비
import tensorflow as tf
x = [[0,0], [0,1], [1,0], [1,1]]
y = [[0], [0], [0], [1]]
- 학습 데이터 저장소 준비
I = tf.placeholder(tf.float32, shape=[None, 2])
V = tf.placeholder(tf.float32, shape=[None, 1])
- 은닉층 뉴런의 가중치와 bias 설정 및 은닉층 뉴런 값 계산
w = tf.Variable(tf.random_normal([2, 1]))
b = tf.Variable(tf.random_normal([1]))
O = tf.sigmoid(tf.matmul(I, w) + b)
- 교차 엔트로피 비용 계산에 의한 가설 검증
cost = -tf.reduce_mean(V * tf.log(O) + (1 - V) * tf.log(1 - O))
- 경사하강법에 의한 가설 수정
optimizer = tf.train.GradientDescentOptimizer(0.1)
train = optimizer.minimize(cost)
- 세션을 만들고 텐서플로우 변수 초기화
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
- 가설을 반복 검증(5000번)하며 w와 b를 학습
for i in range(5001):
sess.run(train, feed_dict={I: x, V: y})
if i % 500 == 0:
print(i, sess.run(w), sess.run(b))
- 학습 모형 테스트
h_infer = sess.run(O, feed_dict={I: x})
print(h_infer)
3. 다층신경망의 기본 학습 원리
"다층신경망의 가중치 학습 원리, 역전파"
은닉층은 출력층이 아니라 출력값을 기반으로 오차를 계산할 수 없다.
3-1. 역전파
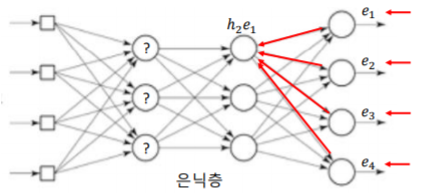
- 은닉층으로부터의 가중치를 계산하는 통계적인 기법
- 기본 아이디어: 출력층의 오차와 연결가중치로부터 은닉층 오차를 역으로 추정
출력 뉴런 결과에 기여하는 것은 이전 뉴런 값의 크기와 연결 가중치다.
이전 뉴런 값이 오차에 영향을 주므로, 오차를 이용하여 추정해 나가는 방식이다.
=> 즉, 현재 뉴런의 에러와 이전 뉴런의 연결 가중치를 가지고 역으로 이전 뉴런의 에러를 추정하는 방법.
3-2. 기본 아이디어
(1) 오차 계산

σi = di - yi
오차 계산은 일반적으로 입력 데이터의 정답에서 출력 뉴런의 산출 결과를 뺀 것과 같다.
(2) 이전 뉴런의 오차값 계산

(3) 첫번째 은닉층까지 오차 계산 반복
3-3. 다층 신경망 학습 과정
1. 신경망의 모든 가중치를 적당한 값으로(랜덤) 초기화
2. 입력 값과 정답으로 구성된 학습 데이터의 입력 부분을 신경망에 입력해 출력 값을 계산
3. 계산된 출력 값과 해당 입력의 정답을 비교해 오차를 계산
4. 출력층 뉴런의 오차를 역전파시켜 바로 이전 은닉층 뉴런의 오차를 계산
5. 4단계를 입력층 앞의 은닉층까지 반복
6. 신경망의 가중치를 차례로 조절
7. 주어진 횟수 만큼 2에서 6단계 반복
3-4. 신경망의 입출력 뉴런 개수
(1) 신경망 분류와 출력층 뉴런 개수

- 이진 분류: 입력 데이터를 2 개의 범주로 분류. 출력 뉴런은 1개
ex. 스팸 메일의 판별(스팸 또는 정상), 대출 승인(승인 또는 거절)
- 다범주 분류: 입력 데이터를 n 개의 범주로 분류. 출력 뉴런은 n개
ex. 동물 분류(사자, 고양이, 호랑이), 색상 분류(빨강, 녹색, 파랑)
(2) 신경망 분류와 입력층 뉴런 개수
신경망 입력 뉴런은 한번에 한 개의 신호만을 전달받을 수 있다. 데이터를 구성하는 특징들 역시 신경망 관점에서는 각각의 서로 다른 신호로 볼 수 있다. 그래서 특징의 개수가 입력 뉴런의 개수가 된다.
3-5. 텐서플로우로 다층신경망 시스템 구성
"배타적 논리합 학습"
배타적 논리합: 입력된 신호가 서로 다를 때 참(1)을 결과로 산출하는 논리 연산
(1) 설계

특징 개수가 2개이므로 입력 뉴런은 2개, 이진 분류이므로 출력 뉴런 1개, 은닉층 1개, 은닉 뉴런 2개
(2) 텐서플로우
- 텐서플로우와 학습 데이터 준비
import tensorflow as tf
x_data = [[0,0], [0,1], [1,0], [1,1]]
y_data = [[0], [1], [1], [0]]
- 학습 데이터 저장소 준비
I = tf.placeholder(tf.float32, shape=[None, 2])
V = tf.placeholder(tf.float32, shape=[None, 1])
- 은닉층 뉴런의 가중치와 bias 설정 및 은닉층 뉴런 값 계산
W1 = tf.Variable(tf.random_normal([2, 2]))
b1 = tf.Variable(tf.random_normal([2]))
h = tf.sigmoid(tf.matmul(I, W1) + b1)
- 출력층 뉴런의 가중치와 bias 설정 및 출력층 뉴런 값 계산
W2 = tf.Variable(tf.random_normal([2, 1]))
b2 = tf.Variable(tf.random_normal([1]))
O = tf.sigmoid(tf.matmul(h, W2) + b2)
- 교차 엔트로피 비용 계산에 의한 가설 검증
cost = -tf.reduce_mean(V * tf.log(O) + (1 - V) * tf.log(1 - O))
- 경사 하강법에 의한 가설 수정
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(cost)
- 세션을 만들고 텐서플로우 변수 초기화
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
- 가설을 반복 검증(50000번)하며 w와 b를 학습
for i in range(50001):
sess.run(train, feed_dict={I: x_data, V: y_data})
if i % 500 == 0:
print(i, sess.run(cost, feed_dict={I: x_data, V: y_data}))
- 학습 모형 테스트
h_infer = sess.run(O, feed_dict={I: x_data})
print(h_infer)
4. 컨볼루션 신경망의 기본 학습 원리
"알파고의 판세 분석"
4-1. 컨볼루션 신경망

- 영상 인식에 특화된 심층 신경망
- 뇌의 시각 피질을 신경망에 차용(시각 피질 + 신경망)
- 특징 추출기와 뉴런으로 구성
4-2. 특징 추출
(1) 기계학습

(2) 이미지와 특징

특징이 많아지면 학습하는 데 사용되는 뉴런이 많이 필요하고 시간이 많이 걸리게 된다.
4-3. 컨볼루션 신경망의 구조

일반 신경망 구성과 비교하여 컨볼루션 신경망에는 '특징추출 신경망' 부분이 있다. 특징추출 신경망 과정은 컨볼루션 단계와 풀링 단계로 이루어져 있다.
4-4. 컨볼루션 단계

- 입력 이미지에서 고유의 특징을 부각시킨 이미지(특징맵)를 새로 생성
- 컨벌루션 필터: 입력한 이미지를 변환시키는 필터
예제

원본 이미지가 4*4 픽셀이라고 가정한 예제이다. 컨볼루션 연산자는 행렬의 곱의 합이다. 2*2 행렬(2*1 행렬 2개)의 컨볼루션 필터를 거치고 나면 결과로 특징맵이 산출된다.
4-5. 풀링 단계

- 원본 이미지의 크기를 줄이는 역할
- 특정 영역의 픽셀들을 묶어 하나의 대표 값으로 축소
4-6. 분류 단계

5. 참고 자료
- 명지대학교 김제민 교수님 강의안
'딥러닝' 카테고리의 다른 글
| [pytorch] 시작하기 (0) | 2019.08.31 |
|---|---|
| 신경망 기초 (0) | 2019.08.27 |
| 신경망 공부하면서 궁금한 것들 셀프 질답 2 (0) | 2019.08.25 |
| 신경망 공부하면서 궁금한 것들 셀프 질답 (0) | 2019.08.24 |
| [tensorflow] 시작하기 (0) | 2019.04.16 |

