Stack Building
[분류] 의사결정나무 본문
1. 의사결정나무 Decision Tree
1-1. 결정 트리 유도에 의한 분류
(1) 결정 트리
- 플로우 차트와 같은 트리 구조
- 내부internal 노드는 속성에 대한 테스트를 나타냄
- 분기branch는 테스트의 결과를 나타냄
- 리프leaf 노드는 클래스 레이블 또는 클래스 분포를 나타냄 (예: buys_computer=Yes)
(2) 트리 생성의 단계
ⓐ 트리 생성
- 처음에는 모든 학습 예제가 루트에 있다.
- 선택된 속성에 기반하여 재귀적으로 파티셔닝partitioning다.
ⓑ 가지치기 Pruning
- 노이즈나 이상치를 보여주는 분기(가지)를 확인하고 제거한다.
(3) 트리 사용
- 알려지지 않은 샘플을 분류한다.
- 의사결정트리에 대해 샘플의 속성값을 테스트한다.
1-2. 예시

1-3. 결정 트리 유도를 위한 알고리즘
(1) 기본 알고리즘: Greedy 알고리즘
- 트리는 하향식 재귀 분할 정복top-down recursive divide and conquer manner으로 구성됨
- 모든 학습 데이터가 루트에서 시작한다.
- 속성은 범주형categorical이다. 연속값continuous은 미리 이산화discretized된다.
- 샘플들은 선택된 속성에 따라 재귀적으로 분할되며, 어떤 포인트에서 자를지, 어떤 것을 루트로 둘지 등은 경험적heuristic/통계적 방법으로 선택된다. 예를 들면 information gain과 같은 것.
(2) 파티셔닝을 중지하는 조건
- 주어진 노드에 대한 모든 샘플은 동일한 클래스에 속해야 한다.
- 추가적인 파티셔닝을 하기 위한 남아있는 속성이 없다. (리프 분류에 majority voting이 사용된다.)
- 더 분류할 샘플이 남아있지 않다.
2. 정보이론 Information Theory
2-1. 동기
- 하나의 문서에 여러 단어가 포함되어 있는 경우를 상정.
- 총 10개의 단어가 '책'은 5번, '기억'은 2번, '학생'이 2번, '학교'가 1번의 빈도로 출현했다면, 문서 혹은 각각의 단어가 제공하는 정보information를 정량적으로 측정하고자 함.
2-2. 정보이론
(1) 정보량
- 메시지의 정보 내용은 주어진 텍스트 내의 단어 출현 확률의 역함수로 측정된다.
- 단어의 출현 확률이 높을수록 더 적은 정보를 가지고 있다고 본다.
- 수식으로 정리하면, p가 단어의 출현 확률일 때 정보량은 아래와 같다.
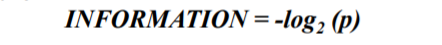
- 중요하면 많이 언급한다는 것이 일반적인 상식인데 이것과 반대인 것처럼 들린다. 이 개념은 정보량을 부호화하는 과정에서 등장하였다. 정보를 파악하고자 할 때 섀넌이라는 사람은 ~인지 아닌지(1과 0, 2가지)로 표현했다고 한다. 어떤 묶음 안에 개체가 16개 있을 때, 그는 4번의 질문으로 그 개체의 정체성을 정확히 판단할 수 있다고 여겼다. 약간 balanced binary search tree에서 탐색을 수행하는 느낌으로 이해했다. 여기에서 정보량이란 개체의 개수가 아니라 질문의 개수이다. 즉 많이 물어봐야 하는 문제, 예측이 어려운 문제, 불확실성이 높은 문제가 정보량이 많은 문제이다! (일반적인 맥락에서도 정보량이 많다고 하면 뭔가 많은 걸 기술한 것을 일컫지 대충 낙서 몇 개 쓴 것을 정보량이 높다고 하지는 않는다.) 즉 모르는 정도에 대한 양이 정보량이며, 이는 엔트로피와 같은 의미이다. 이때 확률은 0과 1 사이의 수로, 여기에 격차를 줄이기 위해 로그를 취하면 음수가 된다. 음수는 절대값이 클수록 작은 수가 된다. 그래서 역함수(-)를 취해 주는 것이다.
예시

- 0.005의 확률로 등장하는 단어는 문서에 덜 등장하는 단어로, 정보량이 많은 단어이다. 50%의 확률로 등장하는 단어의 정보량이 1일 때, 0.5%의 확률로 등장하는 단어의 정보량은 10이다.
(2) 엔트로피
- 문서가 n개의 term으로 특징지어지고, term 각각이 특정한 확률 pk로 발생할 때, 평균average, 엔트로피entropy 또는 기대정보량expected information은 아래와 같은 공식에서 도출된다.

예시
컴퓨터, 메모리, 모니터, 키보드라는 단어의 등장 확률이 각각 0.5, 0.2, 0.2, 0.1이다.
AVE_INFO = -[(0.5log2 0.5) + (0.2log2 0.2)+ (0.2log2 0.2) + (0.1log2 0.1)]
= -[(-0.05) + (-0.46) + (-0.46) + (-0.33)] = 1.3
엔트로피(AVE_INFO)는 용어의 출현 확률이 n개의 별개 용어에 대해 1/n로 동일할 때 최대화된다. 예를 들어 4개의 용어가 모두 0.25의 확률로 등장한다고 하면 엔트로피는 2가 된다. 일란성 쌍둥이들은 이란성 쌍둥이보다 구분하기 어렵다.
3. 분할 Split
3-1. 어떻게 최적의 분할을 결정할까?
- 더 '순수한' 클래스 분포를 가진 노드가 선호된다.
- 때문에 이 문제를 해결하려면 노드의 '불순도impurity'라는 측정치가 필요하다.
- spliting을 할 때에는 엔트로피 매저를 보고 하는데, 순도가 높을수록 엔트로피가 낮아서 좋다.
- 예시: (가: 5, 나:5)인 노드는 불순도impurity degree가 높고, (가:1, 나:9)인 노드는 불순도가 낮다. 후자가 더 pure하기 때문에 이 split을 선호한다.
3-2. 최적의 분할을 찾는 방법
ⓐ 분할하기 전 불순도P를 측정한다.
ⓑ 분할 후 불순도M을 측정한다.
- 각각의 자식 노드에 대한 불순도를 측정
- M은 자식 노드의 가중된weighted 불순도이다.
ⓒ 가장 높은 gain을 산출하는 속성 테스트 조건을 선택한다.
- 즉, 분할 후의 불순도M이 가장 낮은 조건을 선택한다.
- gain = P - M
3-3. 속성 선택값
(1) Information Gain
- 모든 속성은 범주형으로 간주한다.
- 연속형 속성은 변형된다.
(2) 지니 지수
- 모든 속성은 연속형으로 간주한다.
- 각각의 속성에 대해 여러개의 가능한 분할 값이 있다고 가정한다.
(3) Gain Ratio
3-4. 정보 이득Information Gain
(1) 원리
- 가장 높은 정보 이득이 있는 속성을 선택한다.
- P와 N이라는 두 클래스가 있다고 가정할 때, 샘플 셋인 S가 p개의 P 클래스 요소와 n개의 N 클래스 요소를 가진다고 둔다. 이때 S의 임의의arbitrary 예가 P또는 N에 속하는지 결정하는 데에 필요한 정보의 양은 다음과 같다.

(2) 결정 트리 유도에서 정보 이득을 사용하는 방식
속성 A를 사용할 때 집합 S가 {S1, S2 , …, Sv} 로 분할된다고 가정할 때, Si가 pi개의 P와 ni개의 N을 포함하는 경우, 모든 하위 트리 Si에서 오브젝트를 분류하는 데에 필요한 기대정보량 또는 엔트로피는 아래와 같다.

A에서 분기하여 얻을 수 있는 인코딩 정보는 Gain(A) = I(p,n) - E(A)이다.
(3) 정보 이득 계산에 의한 속성 선택 과정

클래스 P는 컴퓨터를 사는 경우(buys_computer = “yes”)이고, 클래스 N은 컴퓨터를 사지 않는 경우(buys_computer = “no”)이다. I(p, n)은 전체 pi의 총합이 9이고 전체 ni의 총합이 5이므로, I(9,5)로 두면 위의 공식에 의해 0.94.으로 계산된다. 나이age 속성에 대한 엔트로피를 계산하면 E(age) = 5/14*I(2,3) + 4/14*I(4,0) + 5/14*I(3,2)가 된다. 따라서 Gain(age)는 I(p,n) - E(age) = 0.246임을 구할 수 있다. 같은 방식으로 Gain(income)을 구하면 0.029, Gain(student)를 구하면 0.151, Gain(credit_rating)을 구하면 0.048이다.
3-5. 지니 지수 Gini Index

만약 데이터셋 D가 n개의 클래스들의 예를 가지고 있다면, 지니지수인 gini(D)는 위와 같이 정의된다. 위의 식에서 pj는 D 안에 있는 j 클래스의 상대적인 빈도(나올 확률)를 말한다. 이진 분류를 할 때, 값이 몰리면 지니지수가 낮아진다.
예시

(1) 노드의 집합Collection에서 지니 지수를 구하는 방법

노드 p가 k개의 자식 노드로 나뉠 경우, 지니 지수는 위와 같이 구한다. 위 식에서 ni는 자식 i가 가지는 레코드의 개수이며, n은 부모 노드 p가 가지는 레코드의 수를 말한다. 자식 노드의 지니지수의 가중 평균이 최소가 되는 속성을 골라야 한다. 가장 작은 GINIsplit(D)를 제공하는 속성(불순도가 가장 낮은)이 노드를 분할하는 데에 사용된다. 각각의 속성에 대해 가능한 모든 분할점spliting points들을 열거할 필요가 있다.
예시

D가 컴퓨터를 사느냐 마느냐에 대한 튜플을 가지고 있는 데이터 집합이라고 하자. 9개의 튜플은 컴퓨터를 산다는 레코드이며, 5개는 사지 않는다는 레코드이다. 그럴 경우 지니 지수의 계산은 위와 같다. 만약 '수입income' 속성이 D를 D1과 D2로 나누는데, D1에는 {낮음low, 중간medium} 속성을 가지는 10개의 레코드가, D2에는 4개의 레코드가 포함된다고 할 때, 지니 지수는 다음과 같이 계산한다.

Gini{low,high}는 0.458이고, Gini{medium,high}는 0.450이다. 따라서 {low,medium}과 {high}로 분리하는 것이 가장 낮은 지니지수를 가지게 되는 것이다.
3-6. 이득 비율Gain Ratio
(1) 더 많은 수의 분할을 할 경우의 문제

노드 불순도 측정은 많은 수의 분할을 더 선호한다. 각 분할은 작지만 보다 순도가 높다. {low, medium}, {high}보다 {low}, {medium}, {high}가 순도가 더 높지 않겠는가. 하지만 너무 많이 분할하면 의미가 없어지기 쉽다. 위의 세 가지 분류에서 고객 아이디로 분류하는 것이 가장 '불순도'가 낮다. 모든 자식 노드에 대한 엔트로피가 0이기 때문에 가장 높은 정보 이득information gain을 얻는다. 하지만 저렇게 분류하는 것은 아무 의미도 없다.
(2) 이득 비율

* 부모 노드인 p는 k개로 분류되며 ni는 파티션 i의 레코드 개수이다.
- SplitINFO는 파티션의 엔트로피로 정보 이득을 조정한다.
- 높은 엔트로피를 가지는 파티셔닝(많은 수의 작은 파티션들)은 불이익을 얻게 된다.
- 정보 이득의 단점을 극복하도록 설계되었다.
- 최대의 이득 비율을 가지는 속성이 분할 속성으로 선택된다.
3-7. 속성 선택값의 비교
정보 이득, 지니 지수, 이득 비율은 일반적으로 좋은 결과를 낸다. 하지만 다음과 같은 단점도 있다.
* 정보 이득: 다중값 속성에 편향된다.
* 지니 지수: 다중값 속성에 편향되고, 클래스 수가 클 때 어려움이 있다. 또한 두 파티션 모두에서 동일한 크기의 파티션과 순도를 보여주는 결과를 선호하는 경향이 있다.
* 이득 비율: 하나의 파티션이 다른 파티션보다 훨씬 작은 불균형 분할을 선호하는 경향이 있다.
3-8. 오버피팅Overfitting과 가지치기Tree Pruning
(1) 오버피팅(과적합)
유도된 트리는 트레이닝 데이터에 너무 적합할 수 있다. 그 때문에 가지가 너무 많거나 노이즈noise나 극단치outlier 때문에 이상anomaly을 보일 수 있다. 또 훈련에 사용된 데이터 외에 사용한 적 없는 샘플unseen samples에 대한 정확도가 낮을 수 있다.
(2) 오버피팅을 피하기 위한 방법
* Prepruning
- 트리 구축을 일찍 중지한다.
- 선량 측정값이 임계값 이하로 떨어지면 노드를 분할하지 않는 방법이다.
- 적절한 임계값을 선택하기 어렵다는 문제가 있다.
* Postpruning
- 완전히 자란 나무에서 가지를 제거한다.
- 학습 데이터와 다른 데이터셋을 사용하여 어떤 것이 '제일 가지치기가 잘 된' 트리인지 판단한다.
3-9. 의사결정나무에 기반한 분류
(1) 장점
- 트리 구축에 비용이 적게 든다.
- 모르는 레코드를 분류하는 데에 아주 빠르다.
- 작은 사이즈의 트리는 해석하기 쉽다.
- 노이즈에 강하다. 특히 오버피팅을 피하는 방법을 적용할 경우.
- 속성들이 서로 상호작용하지 않는 한 중복되거나 관련 없는 속성을 쉽게 처리할 수 있다.
(2) 단점
- 가능한 의사결정나무의 크기space가 기하급수적으로 크다.
(그리디한 접근은 최고의 트리를 찾는 것이 불가능할 수 있다.)
- 속성간 상호작용은 고려하지 않는다.
- 각 결정 경계decision boundary에는 하나의 속성만 포함된다.
4. 앙상블 기법 Ensemble Methods
4-1. 기본 개념
- 학습 데이터로부터 분류기의 집합을 구축한다.
- 여러 분류기의 예측을 결합하여 테스트 레코드의 클래스 레이블을 예측한다.
- perhaps by "voting"
4-2. 앙상블 기법이 작동 가능한 이유

25개의 기본(이진) 분류기가 있다고 가정할 때, 각각의 분류기는 오차율e 0.35를 보이는 경우를 살펴보자. 분류기들의 오류 간에는 상관 관계가 없다고 가정하면 앙상블 분류기가 잘못된 예측을 할 확률은 위 식의 계산값과 같이 0.06으로 아주 줄어든다. 앙상블로 했을 때 잘못된 결과가 나오려면 과반(13) 이상이 잘못 예측해야 하기 때문이다. 잘못 예측한 확률의 13승, 잘 예측했을 확률 12승을 계산한다. 위 그래프에서는 정확도가 0.5이상일 경우 붉은 선만큼 성능이 좋아진다는 것을 보여준다.
4-3. 두 가지 필요조건
(1) 기본 분류기들은 독립
- 기본 분류기가 적은 상관관계가 있는 앙상블 방법에서 분류 정확도가 향상된다.
- 이 조건을 만족하는 것은 어렵기 때문에 최선을 목표로 한다.
(2) 기본 분류기는 랜덤 예측기보다 성능이 좋아야 한다
- 이진 분류기 기준 50% 이상의 성능을 보여야 한다.
4-4. 일반적 접근

(1) 원본 학습 데이터에서 다수의 데이터셋을 만든다
(2) 다수의 분류기를 생성한다
(3) 분류기를 통합한다
4-5. 앙상블 기법의 종류
(1) 데이터 분포 조작
- 샘플링
- 배깅, 부스팅
(2) 입력 피처 조작
- 입력 피처의 부분집합을 선택
- 랜덤 포레스트
(3) 클래스 레이블 조작
- 에러 수정 출력 코딩
(4) 학습 알고리즘 조작
- 의사결정트리를 위한 다른 분할 방법을 제공
- 다른 네트워크 토폴로지를 사용한 신경망
* 비교

- 각 앙상블 기법에 50개의 의사결정나무를 기본으로 사용하고 10겹으로 교차 유효성을 검증할 경우.
- 일반적으로 앙상블 분류기는 하나의 의사결정나무 분류기보다 좋은 결과를 보인다.
5. 랜덤 포레스트 Random Forests
5-1. 랜덤 포레스트란

여러 의사결정나무에 의해 만들어진 예측을 결합한다. 각 트리는 랜덤 벡터들의 독립적인 집합의 값들에 기초하여 생성된다. 여기서 랜덤 벡터는 고정된 확률 분포로부터 생성되며, 의사결정나무를 사용한 배깅 방법은 랜덤 포레스트의 특별한 케이스에 속한다.
5-2. 일반화 오차Generalization Error

- 에러의 기대치, upper bound
- p가 나무들 사이의 상관 평균이고, s는 나무 분류기들의 '강도'를 측정하는 측정치다. 따라서 1-s는 약한 정보가 나온다. 여기에 p를 곱하고 평균을 만들어주면, 평균적인 상관 정도를 알아낼 수 있는데, 이 정도가 높으면 좋지 않다. 상관 정도가 작아지면 오차도 낮아지고, 훌륭한 모델이 만들어질 확률이 높아진다.
- 나무들의 상관관계가 높아지거나, 앙상블의 강도가 줄어들면 일반화 오차는 증가한다.
- 무작위화Randomization는 나무들 간의 상관관계를 줄이는 데 도움을 주어 앙상블의 일반화 오차를 개선하는 데에 도움을 준다.
- 분류 집합의 '강도'는 분류기의 평균 성능을 뜻한다.

- Y^Θ는 어떠한 랜덤 벡터 세타로부터 만들어진 분류기에 따라 예측된 클래스 X이다. 마진이 클수록 분류기가 주어진 샘플 X를 잘 분류했다는 것이다. 마진은 갭이다.
5-3. 랜덤 벡터 생성
(1) Forest-RI (랜덤 인풋 선택)
- 가장 많이 쓰인다.
- 전체 인풋 피처 d개를 전부 고려하기에 너무 많을 때, 무작위로 F개의 입력 피처를 선택하여 결정트리의 각 노드에서 분할한다. 예를 들어 120개 중 5개만 고르는 식이다. 이때, replacement는 할 수도 안 할 수도 있다. 일단 f를 결정한 후에는 일반 의사 결정 나무와 같다. f가 서로 무작위 추출 되므로 각 나무들의 피처는 다를 수 있다.
- 노드를 분할하는 결정은 선택된 F개의 피처들로부터 결정된다.
- 가지치기pruning는 하지 않는다.
- 예측은 다수결 투표 방식majority voting을 사용하여 결합된다.
(2) F(피처의 수)에 대한 트레이드 오프
- 피처의 수가 작으면 트리들은 서로 덜 상관 있어진다.
- 단 피처의 수가 크면 강력한 분류기가 된다. 상관정도를 작게 할 것인지, 강도를 높일 것인지 선택해야 한다.
- 일반적인 선택은 F = log2d + 1
(3) Forest-RC (랜덤 조합)
- 원본 피처 수인 d가 너무 작을 때 사용한다.
- d보다 작은 f를 뽑으려는데 그게 잘 안 되면 랜덤화가 잘 안 되기 때문에 억지로 피처를 늘리는 것이다.
- 입력 피처의 선형 조합을 생성한다.
- 현업에서는 잘 쓰이지 않는다
(4) 3차 접근
- 무작위로 결정트리의 각 노드에서 F개의 가장 좋은 분할을 선택한다.
- f개를 랜덤하게 뽑아 최적의 분할을 찾는 것. 앞과 앞뒤가 바뀌었다. 미리 f개를 선정한 것. 다만 최적의 경우는 한정적이다.
- Forest-RI와 RC방식보다 상관관계가 더 높아질 수 있다.
- 런타임 절약saving이 없다. 결정트리의 각 노드에서 분할 피처를 확인해야 한다.
* 랜덤포레스트에 대한 분류 정확도는 AdaBoost 알고리즘과 꽤 유사하다.
* AdaBoost 알고리즘보다 훨씬 빨리 돌아가고, 노이즈에 강하다.
6. 참고자료
1. 명지대학교 <인공지능> (전종훈 교수님) 강의안
2. 정보이론
3. 정보량
4. 정보 엔트로피
5. 정보이론 기초
6. 네트워크 토폴로지
7. 의사결정트리의 인코딩
'머신러닝' 카테고리의 다른 글
| k-fold 교차 검증 (0) | 2019.05.26 |
|---|---|
| 선형회귀 (0) | 2019.05.26 |
| [분류] 베이즈 분류 (0) | 2019.05.25 |
| [python] 데이터시각화 (0) | 2019.05.13 |
| [aws] lamdba (0) | 2019.04.17 |




