Stack Building
선형회귀 본문
1. 회귀와 분류의 차이
분류는 지도학습, 클러스터링은 비지도학습이다. 다만 지도학습이 모두 분류는 아닌데, 바로 지도학습에 '회귀Regression'가 있기 때문이다. 회귀 문제는 연속적continuous인 값을 예측한다. 입력값을 어떤 연속함수에 매핑한다. 부동산 시장의 주택 매물의 크기 데이터가 주어지고, 그 주택들의 가격을 예측하는 문제가 회귀의 예라고 볼 수 있다. 분류는 이산값discrete categories을 예측한다. 입력값을 이산 카테고리(ex. 긍정/부정)로 매칭한다. 종양을 가진 환자의 데이터를 주고 이 종양이 악성인지 양성인지 예측하는 것이 그 예이다. (로지스틱 회귀는 분류이다)
2. 선형회귀
2-1. 예시

선형 회귀란 독립 변수와 종속 변수의 선형 상관 관계를 모델링하는 것이다. 직관적으로 말해 데이터의 분포를 잘 설명할 수 있는 직선을 찾아내어 데이터에 존재하지 않는 독립 변수 값에 대한 종속 변수를 예측하는 것이다.
위에서 한번 언급한 부동산 가격 예측을 선형회귀의 예로 살펴볼 수 있겠다. 이는 데이터 안의 각 예 안에 '올바른 답'이 주어진 지도학습이다. 동시에 실수값real-valued을 출력치로 예측하는 회귀 문제이다. 출력치의 데이터형(연속,실수값 OR 이산값)은 회귀와 분류를 구분하는 기준이다. 타깃 변수가 연속적이면, 우리는 그 학습 문제를 회귀 문제라고 부른다.
2-2. 특징
(1) 학습 세트 Training Set
주택 가격의 학습 데이터는 다음과 같다.

m은 학습 데이터 예제들의 총합이다. x는 '입력input' 변수(또는 피처)이고, y는 '출력output' 변수(또는 '타깃' 변수)이다. (x,y)는 하나의 학습 예제이고, (x^(i), y^(i))는 i번째 학습 예제를 가리킨다. x^2와 같은 표기와 구분하기 위해 사용한다. 쉽게 말하면 총 m개의 레코드를 가진 학습 데이터 (x,y)는 독립변수/입력변수/피처인 x와 종속변수/출력변수/타깃인 y로 이루어져 있으며, 각 레코드는 (x^(i), y^(i))와 같이 표기한다.
(2) 지도 학습

지도 학습 문제를 대할 때, 우리의 목표는 주어진 학습 데이터셋을 가지고 함수 h를 학습하는 것이다. h는 X->Y의 형태이며, h(x)는 y의 해당값에 대한 '좋은' predictor가 되어야 한다. 전통적으로 이 함수 h는 가설hypothesis이라고 불린다. 이 과정을 도식화한 것이 위 그림인데, 학습 데이터로 -> 알고리즘을 학습하여 -> 함수 h를 찾아내는 것을 확인할 수 있다. x(주택의 거주 면적)을 이 함수 h에 집어넣으면, 예측한 y값(예측된 주택 가격)을 출력한다. 이 h를 표현하는 방법을 간단하게는 h(x)라고 하고, 공식적으로는 hΘ(x) = Θ0 + Θ1x 라고 표현한다. 이와 같이 하나의 변수를 사용한 선형 회귀를 단변량 선형 회귀Univariate linear regression라고 부른다.
2-3. 비용 함수Cost Function

가설 식이 hΘ(x) = Θ0 + Θ1x일 때, Θi는 파라미터이다. 파라미터를 어떻게 주느냐에 따라서 직선 h(x)의 모양은 크게 달라진다. 그렇다면 우리는 어떻게 이 파라미터를 선택해야 할까? 가능한 가장 좋은 직선(h)을 우리가 가진 데이터에 fit시키는 방법은 무엇일까? 소제목에서 보이다시피, 비용 함수를 사용하면 된다.
비용 함수란 '비용이 얼마나 있는지'를 나타내는 함수다. 여기서의 비용은 바로 오류를 말한다. 쉽게 생각해도 오류를 수정하려면 비용이 많이 들기 마련이다. 모델을 학습할 때 오차는 작을수록 좋다. 즉 모델 학습은 비용을 최소화하는 방향으로 진행된다. 비용이 최소화되는 곳이 성능이 가장 잘 나오는 부분으로, 가능한 비용이 적은 부분을 찾는 것이 바로 최적화Optimization이고, 일반화Generalization이다. 지금은 선형 회귀 문제를 다루고 있으므로 비용 함수는 직선에서 데이터가 얼마나 떨어져 있는지를 계산하는 함수이다.

위 그림에서 J(Θ0, Θ1)이 바로 비용 함수이다. 우리의 학습 데이터 (x,y)에 대해 hΘ(x)가 y에 가까워지도록 Θ0, Θ1를 선택해야 한다. 가까워진다는 것은 곧 오차가 적다는 의미이다. 오차가 적다는 것은 hΘ(x)가 핏 되고 싶어하는 y와 차이가 얼마 나지 않는다는 뜻이다. 즉, 둘의 차이가 비용이고, 둘의 차이를 구하는 것이 비용 함수이며, 비용이 최소가 되어야 하므로 비용 함수값(J(Θ0, Θ1))이 최소가 되는 Θ0와 Θ1을 구해야 한다는 것이다. 그냥 hΘ(x)-y를 하면 될 것을 왜 굳이 제곱을 하는 이유는 양수로 값을 바꾸기 위해서이기도 하고, 값을 '뻥튀기'하여 차이를 극명하게 하기 위해서기도 하다. 여기에서 error를 제곱square하기 때문에 이 방법을 Squared Error Function이라고 부른다. (비용 함수는 여러 가지가 있다!) 총 m개 각각의 hΘ(x)와 y의 차이를 구하고 나서, 전부 더하고 난 뒤에 1/2m을 해준다. 1/2를 해주는 이유는 미분을 했을 때 나오는 2를 제거하기 위해서이고, 1/m을 해주는 이유는 squared error에 대한 mean을 얻기 위해서이다. 그래서 이 공식을 흔히들 평균제곱오차MSE라고 부른다.
2-4. 경사 하강Gradient Descent
(1) 목적

비용 함수 J(Θ0, Θ1)이 있을 때 (또는 J(Θ0, Θ1, Θ2, ..., Θn)) 비용 함수로 우리가 하고자 하는 것은 minΘ0, Θ1J(Θ0, Θ1)이다. 다시 말해, 비용함수 J를 최소화하는 Θ0, Θ1의 값을 알고 싶은 것이다. 최소값을 찾아가는 방법은 처음에는 어떤 Θ0, Θ1로 시작(ex. Θ0=0, Θ1=0)하여, 최소값에 다다랐다고 여겨질때까지 J(Θ0, Θ1)가 줄어들도록 Θ0, Θ1 값을 계속 수정하는 것이다. 선형 회귀에서 비용함수 J를 최소화하는 알고리즘은 '경사 하강법'이라고 부른다.
Θ0, Θ1, J(Θ0,Θ1)을 그래프로 그린 것이 위 그림이다. 붉은 부분(J가 높은 부분)이 안 좋은 부분이고, 푸른 부분(J가 낮은 부분)이 좋은 부분이다. 푸른 색이 짙을수록 좋다. 이렇게 한 눈에 어디가 가장 좋은지 알 수 있으면 좋겠지만 일반적으로는 그렇지 않다. 일반적으로 제일 낮은 'global minimum'을 찾을 수 있으리라는 보장은 없다.
(2) 알고리즘

경사 하강법의 알고리즘을 수식으로 표현하면 위와 같다. :=는 할당한다는 의미의 수학적 기호이다. 수렴할 때까지 각 Θ의 값을 반복적으로iterative 조정하되, 그 방식은 이전 Θ값에서 Θ에 대하여 편미분한 이전 비용함수를 학습율과 곱한 값을 빼준 값을 할당하는 것이다. 편미분은 특정 변수를 제외한 나머지를 상수로 생각하여 미분하는 것을 의미한다. 각 Θ값은 동시에simultaneous 업데이트 되어야 한다. 당연한 말이다. incorrect한 방식으로 할 경우 다른 Θ값이 바뀌어 Θ1을 구할 때의 J가 변할 것이다. Θ의 총 개수가 n개라고 하면, n개를 동시에 업데이트해주어야 한다.
global minimum을 찾는 데 주요한 영향을 미치는 것은 1.초기값 설정, 2. 알파(학습율)의 크기다.
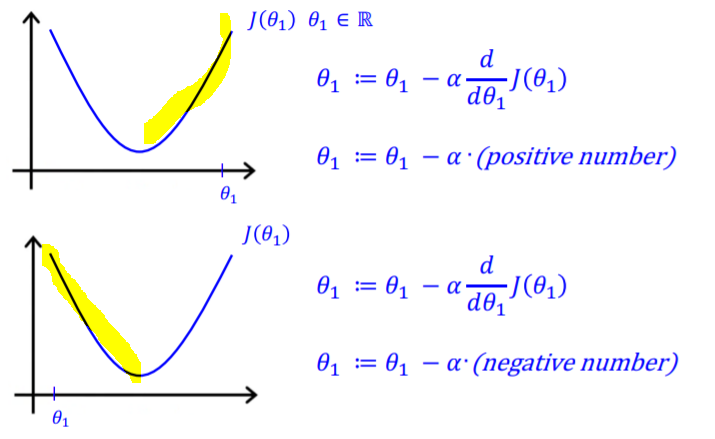
직관적으로 보다 단순한 경우를 가정해보자. 하나의 매개변수로 비용함수를 최소화하고 싶을 때, 경사 하강법 알고리즘은 위와 같다. 초기값이 global minimum보다 클 경우, Θ에서 학습율*양수를 뺀 값을 할당하게 되고 초기값이 global minimum보다 작을 경우 Θ에서 학습율*음수를 뺀 값을 할당하게 된다. 그러면 전자의 경우에는 Θ가 점점 작아지고, 후자의 경우에는 Θ가 점점 커져서 결과적으로 global minimum에 가까워지게 된다.
(3) 학습율learning rate

*알파=학습율
즉 알파값이 너무 작으면 경사 하강은 느리게 일어난다. 알파가 너무 크면 경사 하강은 최소값을 놓칠 수 있다. 그러면 수렴하지 못하게 되거나 발산할 수도 있다. 학습율은 적절한 값을 줘야 한다. 알파값은 0.001 -> (0.003) -> 0.01 -> ... 등의 값을 줘가며 추이를 지켜본다.
(4) Local Minimum Problem

경사 하강법이 막강한 것은 아니다. local minimum 문제가 생길 수 있다. 위와 같은 경우에서 local optima 부분 역시 기울기가 0으로, 경사하강법 알고리즘은 J값이 0이 되므로 여기서 수렴한다고 여긴다. 그러나 왼쪽에 더 낮은 부분이 있다. global minimum을 찾지 못하고 local minimum에서 경사 하강이 멈춰 버리는 문제를 local minimum 문제라고 한다.
학습율 a가 고정되어 있어도 경사하강법 알고리즘은 local minimum으로 수렴할 수 있다. 알파를 처음엔 크게 나중엔 작게 수정하는 방법도 큰 의미가 없다. local minimum에 가까워질수록, 편미분값이 저절로 줄어들어 경사하강법 알고리즘이 자동으로 더 작은 step을 밟기 때문에 학습율을 조정할 필요가 없다.
(5) 선형 회귀를 위한 경사 하강법

Batch Gradient Descent
* batch: (다발) 경사하강의 각 단계는 모든 학습 데이터를 사용한다. m개의 학습 데이터가 있으면 m개를 다 본다. 몇 개만 보는 게 아니라 통으로 한꺼번에 다 본다. (cf. 일부만 하는 것은 mini batch)
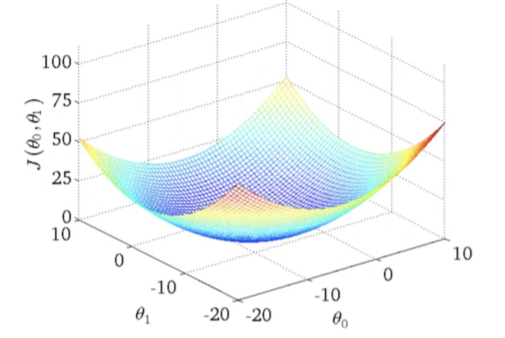
선형 회귀에서 쓰이는 비용 함수는 항상 "볼록함수Convex Function"이다! 오목한 바닥이 하나인 함수이기 때문에, local minimum이 없고 global minimum만 존재하므로 걱정하지 않아도 된다.
3. 요약
비용 함수의 최소값을 찾는 문제를 해결하는 방법에는 반복 알고리즘인 '경사 하강법'과 '일반 방정식 방법'이 있다. 여러 단계로 기울기를 바꿔보지 않고 비용 함수의 최소값을 수학적 수식을 통해 수치로 바로 풀어낼 수 있는 방법이다. 경사 하강법은 후자보다 더 큰 데이터셋을 다룰 수 있어 확장성 면에서 더 좋다. 경사하강법의 일반화된 방법은 더 강력하게 만든다.
4. 참고 자료
1. 명지대학교 전종훈 교수님 강의안
4. 편미분
5. 볼록함수
'머신러닝' 카테고리의 다른 글
| [분류] 로지스틱 회귀 (0) | 2019.05.26 |
|---|---|
| k-fold 교차 검증 (0) | 2019.05.26 |
| [분류] 의사결정나무 (1) | 2019.05.26 |
| [분류] 베이즈 분류 (0) | 2019.05.25 |
| [python] 데이터시각화 (0) | 2019.05.13 |




