Stack Building
[분류] 로지스틱 회귀 본문
1. 로지스틱 회귀
1-1. 분류

이메일을 스팸과 일반 메일로 구분하고, 온라인 상거래의 이상치를 검토하고, 종양이 양성인지 음성인지 분류해주는 예제를 보아 왔다. 이처럼, 분류에서 종속 변수 y는 0과 1 중에 하나가 되었다. 0은 부정적이고, 1은 긍정적인 경우, 단 두 가지로 말이다. 그런데 이때, y가 두 개가 아니라 여러 개로 분류되는 것을 multiclass problem이라고 부른다.
1-2. 선형회귀Linear Regression의 문제점

위와 같은 분류를 선형회귀로 나타내면 어떻게 될까? 위의 분류기는 임계값 분류기Threshold classifier로, 임계치 이상의 값은 a, 아닌 것은 b 와 같은 식으로 분류를 수행한다. 만약 임계값 분류기 hΘ(x)가 0.5보다 크거나 같으면 y는 1이고, 작으면 y가 0이라고 한다면, 그래프를 선형으로 그리기 상당히 곤란해진다.
cf. 임계값: 미적분학에서 임계값은 경계와 비슷한 개념이다. 어떤 변화가 나타나기 시작하는 지점을 일컫는다.
* classifier = estimation = hypothesis = hΘ
1-3. 로지스틱 회귀Logistic Regression개념
Classification: y = 0 or 1
hΘ(x) can be > 1 or < 0
Logistic Regression: 0 ≤ hΘ(x) ≤ 1
로지스틱 회귀는 그래서 등장했다. 분류 결과가 0또는 1이 나오는데, 분류기 hΘ(x)는 0보다 작거나 1보다 클 수 있는 경우에 사용하며, 로지스틱 회귀를 사용하면 hΘ(x)의 값은 0과 1 사이에 위치한다. 따라서 로지스틱 '회귀'는 '분류' 알고리즘이다. 예측 결과가 확률이기 때문에 아무리 커져도 1 이상 커지지 않고 아무리 작아도 0 미만으로 떨어지지 않는다.
1-4. 가설Hypothesis의 표현Representation과 산출물 해석
(1) 가설의 표현

분류 문제를 다룰 때 가설을 표현할 함수는 '시그모이드 함수', 다른 말로 '로지스틱 함수'라고 부른다. x=0일 때를 기준으로 y값이 0 또는 1로 구분된다. 선형회귀에서 hΘ(x)=Θ^Tx였다면, 로지스틱회귀에서는 hΘ(x)=g(Θ^Tx)이다. 이 g(z)가 바로 활성 함수, 로지스틱 함수인 '시그모이드 함수'이다.
예시

x가 위와 같이 주어진 벡터일 때를 가정하자. 1이 악성(양성)인 경우이고, 0이 음성인 경우이다. 주어진 벡터 x는 x0, x1이라는 두 개의 피처를 가지고 있고, x0은 악성인 경우인 1이 들어가고, x1에는 종양의 사이즈가 들어간다. 이때, hΘ(x)는 0.7이 나오므로 환자에게 종양이 악성일 확률이 70%라고 말할 수 있다. hΘ(x)란 결국 Θ로 파라미터화된 x가 주어질 때, y=1일 확률을 구하는 것이다. y는 0또는 1이므로, 주어진 조건에서 y=0일 확률과 1일 확률을 더하면 1이 된다.
2. 결정 경계Decision Boundary
2-1. 로지스틱 회귀 다시보기

그림 하나로 정리해보면, 결국 로지스틱 회귀란 위와 같다. 예측할 때에는 hΘ(x)의 값이 0.5이상인지 아닌지에 따라 1또는 0으로 분류된다. Θ^Tx가 0이상이기만 하면 언제나 hΘ(x)가 0.5이상이 된다.
2-2. 결정 경계Decision Boundary
(1) 선형

결정 경계가 선형으로 가능할 때를 살펴보자. 위의 예시에서 결정 경계는 x1+x2=3이라는 직선이다. 익숙한 방식으로 표기하면 x2=-x1+3이다. (y=ax+b의 식) 이 경계선의 위에 있으면 1, 아래에 있으면 0으로 예측하는데, 위와 아래라는 말을 표현하는 방법이 바로 부등호/부등식이다.
(2) 비선형

하지만 항상 데이터를 직선으로 분리할 수는 없으므로, 결정 경계가 비선형일 때도 살펴보자. 위의 예제에서 결정 경계는 x1^2+x2^2=1이다. 이 식은 기하학에서 원의 방정식이라는 이름으로 접해본 적이 있다.
위의 두 가지 경우에서 어떻게 결정 경계의 식을 찾아낸 것일까? 답은 바로 Θ이다. 로지스틱회귀식은 hΘ(x)로, 우리가 알아야 할 것은 바로 최적의 Θ값이다. 트레이닝 세트는 파라미터인 Θ의 값을 fit 하기 위해 사용되고 파라미터 값을 알고 나면 트레이닝 세트는 더 사용하지 않는다. 한번 우리가 파라미터 Θ의 값을 찾았다면, 그것이 바로 결정 경계를 정의하는 것이 된다.
위의 경우들을 살펴보면 Θ값이 주어진 경우, 즉 0이 아닌 경우만 살아남아 결정 경계식을 이루고 있다. 만약 아주 복잡한 hΘ(x)가 있어서 x의 차수가 비현실적으로 엄청나게 많더라도 fit 한 결과에서 많은 Θ값을 결정하고 나니 다수의 항이 사라진다면 결정 경계식은 그보다 간단할 수 있다.
3. 비용 함수Cost Function
3-1. 어떻게 파라미터를 fit 하는가?
(1) 객체들을 최적화한다.
(2) 비용함수: 파라미터들을 fit 하는 데 사용한다.
3-2. 문제 다시보기
m개의 트레이닝 세트가 있다. 이 트레이닝 세트는 (x^(i), y^(i))의 튜플의 집합이다. x^(i)는 x0=1이고 n개의 피처를 가진(xn까지 존재하는) 벡터이다. y^(i)는 {0,1}의 원소이다. 즉 로지스틱회귀의 경우이며, hΘ(x)는 g(Θ^Tx)이다. 이 경우, 파라미터 Θ는 어떻게 골라야 하는가?
3-3. 비용 함수
(1) 선형 회귀
"예측값과 실제값의 오차를 제곱한 모든 값의 평균"
비용함수 J(Θ)

비용 Cost

선형 회귀식을 y=ax+b로 익숙하게 만들어서 살펴보면, 사실 가장 중요한 파라미터는 a이다. 전체 데이터가 그래프 상에서 어떤 기울기의 직선과 유사한지를 보는 것이기 때문이다. b는 사실 ax의 오차를 보정하는 일을 한다. 선형회귀의 비용함수는 선형회귀에서 가장 적절한 a,b의 값을 찾는 과정에서 변화하는 a,b의 값을 검증하는 데에 쓰인다. 검증이라는 말을 풀어 쓰면 "내가 예측한 y와 실제 y의 오차를 살펴보는 일"이 된다. 그래서 내가 예측한 y인 h(x^(i))와 y^(i)를 일단 빼 준다. 그런데 이 값을 그냥 사용하면 부호가 달라져 평균값을 구하는 데에 어려움이 생긴다. 그래서 양정수로 만들기 위해 이를 제곱한다. 오차가 클수록 제곱값이 커지기 때문에 패널티로 작용한다. 하나의 튜플에 대해서만 이런 작업을 수행하면 안 되니까 이제 모든 튜플에 대해서 같은 과정을 반복한다. 튜플의 총 개수가 m개였기 때문에 m개에 대하여 전부 더해준 후, 평균을 알아보기 위해 m으로 나눠준다.
* 1/2은 넣어도 되고 안 넣어도 되는데, 계산의 편의를 위한 부분이다.
* 선형 회귀의 비용함수는 squared error function
(2) 로지스틱 회귀

위와 같은 경우에서는 x의 차수가 1이기 때문에 비용함수 결과가 2차식이다. 오목함수로 결과가 나와 global minimum을 구하는 데에 무리가 없다. 그러나 만약 x의 차수가 커진다면, non-convex한 모습이 나와 local minimum을 가지게 될 것이다. 이를 잘 다듬어서 convex한 형태로 cost function을 만들기 위해 도입한 방식이 바로 "log"이다.
비용함수

비용

- 로지스틱 회귀에서 비용을 구하는 방법은 로그식을 사용하는 것이다. 위의 비용함수는 J(Θ)가 로지스틱 회귀에 대해 "convex"함을 보장한다.
- y=1이면 왼쪽 그래프를 본다. h(x)가 1이면 y는 0이 되어 비용도 0이다. h(x)가 0이면 y가 무한대가 되어 비용 모두 무한대가 된다. y=0이면 오른쪽 그래프를 본다. y=0일 때에는 h(x)가 1이면 y와 비용 모두 무한대이고, h(x)가 0이어야 y와 비용은 0이 된다.
- y는 실제 데이터고 h(x)는 y의 예측값이라 맞을 수도 있고 틀릴 수도 있다. y가 1일 때 비용이 적으려면(0) h(x)도 1에 가까워야 한다. h(x)가 1이면 딱 맞겠지만(비용이 0) 보통 그렇지 않고 0과 1 사이의 값이 된다. 선형 회귀 때처럼 패널티를 주기 위한 제곱은 하지 않는다. 로그 자체에 패널티와 동일하게 무한대로 수렴하게 하는 값이 있어서다. 결론적으로 선형 회귀처럼 분류에서도 비용이 최소가 되도록 W를 조절하는 것이 핵심이라고 볼 수 있겠다.
4. 간단하게 만든 비용 함수
4-1. 로지스틱 회귀의 비용 함수

3-3-(2)에서 구한 로지스틱 회귀의 비용을 구하는 식을 간단하게 한 줄로 표현하면 위와 같다. y=1일 때에는 -log(hΘ(x))이고, y=0일 때에는 -log(1-hΘ(x))를 구하면 된다. 위의 비용 구하는 식을 적용한 비용 함수 식은 아래와 같다.

어떻게 효율적으로 다른 모델들에 대한 파라미터의 데이터를 찾아낼 수 있는가에 대한 통계적 아이디어인 "최대우도추정maximum likelihood estimation"의 원리를 사용했다. 이는 "convex"하다! 계속 convex함을 강조하는 이유는 덕분에 global minimum으로 수렴converge하여 찾아내기 쉬워졌기 때문이다.
4-2. 파라미터 fitting
비용 함수는 로지스틱 회귀 모델을 fitting할 때 사용한다. 파라미터 fitting은 다음과 같은 과정으로 진행된다.
(1) 파라미터 Θ를 fit : 비용함수 J(Θ)를 minimize하는 Θ를 찾는다
(2) 새로운 x를 주어 예측을 수행한다. 이때의 output은 P(y=1, x;Θ) 즉 hΘ(x)이다.
4-3. 경사 하강Gradient Descent ★
이제까지 하나하나 모든 값을 넣어 보며 비용함수값을 최소로 만드는 Θ를 찾아왔지만, 현실 세계의 데이터량이 어마어마하기 때문에 사실 이것은 실제로는 불가능에 가깝다. 따라서 선형 회귀에서도 다뤘던 경사 하강법을 통해 Θ를 찾기로 한다.
minΘ J(Θ):
Repeat {
Θj := Θj - a* o/oΘj * J(Θ)
(동시에 모든 Θj가 업데이트됨)
}
이는 위와 같은 알고리즘으로 표현할 수 있다. 여기에서 Θ는 Θ0~n까지의 벡터이고 a는 learning rate로, scaling을 위한 값이며 :=이라는 기호는 할당한다는 뜻이다. 위 알고리즘에서 o/oΘj 부분은 Θj에 대해 편미분한다는 의미이다. repeat 블록 안의 수식을 바꿔 쓰면 아래와 같다. 이 알고리즘은 선형 회귀의 것과 hΘ(x) 부분을 빼면 아주 유사하다.

4-4. 구현하기implementation
(1) For 루프 vs 벡터화
- m+1개의 파라미터를 한번에 모두 업데이트 가능하다.
(2) 피처 스케일링
- 피처들이 아주 다른 크기일 때 사용한다. (예: {A: 0-15, B:20-3000})
- 선형회귀 뿐 아니라 로지스틱 회귀에서도 경사하강이 빠르게 수렴할 수 있도록 도와준다.
(3) 로지스틱 회귀는 아주 강력하고 많이 사용되는 알고리즘이다.
5. Multiclass Classification
5-1. 예시
(1) 이메일 폴더 분류/태그하기 : 일, 친구, 가족, 취미 등
(2) 의학 진단: 아프지 않다, 감기, 독감 등
(3) 날씨: 맑다, 흐리다, 비가 온다, 눈 등
5-2. 이진binary 분류와의 비교

5-3. One-vs-All (또는 One-vs-Rest)

클래스 1, 2, 3의 모음 안에서 클래스 1만 분류해내는 것을 목표로 한다. 로지스틱 회귀 분류기인 hΘ^(i)(x)를 각각의 클래스 i에 대해 학습시키고, y=i가 되는 확률을 예측한다. 새로운 인풋 x에 대해 예측하려고 할 때에는 max i hΘ^(i)(x)를 maximize 하는 클래스 i를 고르게 된다.
6. 정규화Regularization
"과적합 문제를 줄여보자!" Reduce the overfitting problem!
6-1. Overfitting의 예시

위 그림은 주택 가격에 대한 선형 회귀 모델이다. 우리가 너무 많은 피처를 가지고 있을 때, 학습된 가설은 트레이닝 세트에 아주 잘 맞을 수 있지만 새로운 예에 대해 일반화하는 것에 실패할 수 있다. 로지스틱 회귀에서도 마찬가지다.

6-2. 과적합 문제 해결 Addressing Overfitting
일반적으로 가설을 플라팅plotting하는 것은 어떤 다항식을 사용할지 결정하는 하나의 시도가 될 수 있다. 하지만 너무 많은 피처를 가지고는 데이터를 플라팅하기도 힘들고, 시각화하기도 힘들며, 어떤 피처를 keep하고 어떤 피처를 신경 쓰지 않을지를 결정하는 것도 힘들다. 피처의 수가 아주 많은데 학습 데이터의 개수는 적으면, 과적합이 문제가 될 수 있다. 과적합 문제를 다루기 위해 일반적으로 취하는 조치에는 두 가지가 있다.
(1) 피처의 개수 줄이기
- keep할 기능을 수동으로 선택한다.
- 모델 선택 알고리즘: 자동으로 어떤 피처를 keep할지 결정한다.
- 일부 피처를 버리는 것은 문제에 대해 가지는 정보 중 일부를 버리는 것과 같다. 예를 들어 집값 예측에는 실제로 정말 어마어마한 양의 피처들이 필요할지 모른다.
(2) 정규화
- 모든 피처를 유지하되, 파라미터의 크기/값을 줄인다.
- y를 예측하는 데에 약간이라도 기여하는 많은 피처를 가지고 있을 때 예측은 좀 더 잘 작동한다.
6-3. 직관적인 예시
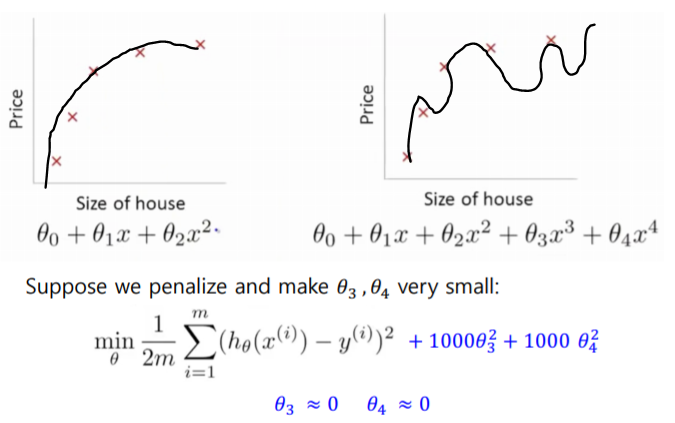
Θ3과 Θ4를 아주 작게 만들려면 패널티를 주면 된다. 비용 함수를 계산할 때 해당 요소에 아주 큰 값을 줘버리면 minimize 하기 위해 해당 요소는 거의 0에 가까운 값이 된다. 파라미터의 값이 적게 들어가면 오버피팅이 될 확률이 줄어든다! 이 파란 글씨 부분을 정규화 과정이라고 보면 된다. 이렇게 그래프가 '부드러워' 져서, 이 과정을 smoothing이라고 부른다.
6-4. 정규화

파라미터 Θ들에 대해 작은 값들을 준다. 가설을 "간소하게" 만드는 것이다. 과적합되는 경향이 적다. 이 방법은 L2 정규화라고 불린다. 여기에서 람다는 "정규화 파라미터"라고 한다.
6-5. 정규화 파라미터

정규화된 선형회귀에서 우리는 J(Θ)를 최소화하는 Θ를 골랐다. 만약 람다가 10의 10승과 같이 문제에 비해 너무 커다란 값이라면 식은 underfit된다. 언더피팅과 오버피팅 사이에 적절한 값을 잡아야 한다.
7. 정규화된 로지스틱 회귀 Regularized Logistic Regression
7-1. 개념

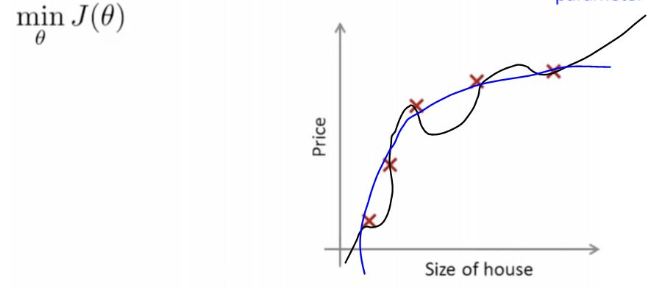
위 그림과 같은 상황에서 로지스틱 회귀식은 왼쪽의 hΘ(x)이고, 비용 함수는 J(Θ)이다. 이를 정규화하면 오른쪽과 같이 람다식이 추가된다.
7-2. 경사 하강 ★

경사하강을 쓰면서 loop로 세타를 조정해가며 글로벌 옵티멀 미니멈을 찾는다. 러닝레이트 알파와 m 모두 작은 값이다. 알고리즘에서 알 수 있다시피 특정 세타만을 작게 만들기는 어렵다. 전체를 조금씩 작게 해야 한다.
8. 실습
sklearn의 패키지 안에 로지스틱 회귀의 모델이 들어있다. 정규화가 기본으로 제공되며, L1(Lasso)과 L2(Ridge)의 방식이 조금 다르다. 파라미터는 패널티, Solver, max_iter 등이 있다. 패널티의 디폴트는 L2이고, 최적화 문제에 사용되는 알고리즘인 Solver에는 Sga(Stochastic Average Gradient descent)과 Saga(Variant of Sga) 그리고 Liblinear가 있다. 마지막 알고리즘이 기본값이며, 이는 규모가 큰 선형회귀를 위한 라이브러리로, Coordinate Descent 알고리즘을 사용한다. max_iter의 기본값은 100으로, 수렴을 위한 반복 횟수의 최대값이다. 여기에서 차원 축소를 하는 방법은 minimum df 제한인데, 자주 출현하지 않는 토큰을 분석에서 제외하여 피처를 줄이는 것이다.
9. 참고 자료
1. 명지대학교 전종훈 교수님 강의안
2. 임계값의 정의
3. 선형회귀분석 함수정리
4. coursera - machine learning week 3
5. 최대우도추정 (★)
6. 편미분 수식 읽기
'머신러닝' 카테고리의 다른 글
| 텍스트마이닝 (0) | 2019.06.01 |
|---|---|
| [분류] SVM (0) | 2019.06.01 |
| k-fold 교차 검증 (0) | 2019.05.26 |
| 선형회귀 (0) | 2019.05.26 |
| [분류] 의사결정나무 (1) | 2019.05.26 |




