Stack Building
[분류] SVM 본문
1. Support Vector Machines

서포트 벡터를 사용하는 방법. 아주 강력하고 많이 쓰이는 방법이다. 복잡한 비선형 함수(로지스틱 회귀 등)를 학습하는 더 깔끔하고 강력한 방법을 제공한다. SVM의 가장 큰 특징 두 가지는 목표objective를 최적화한다는 것과 큰 마진을 가지는 분류기라는 것이다.
2. Optimization Objectives
2-1. 로지스틱 회귀와의 비교

로지스틱 회귀는 1과 0으로 분류하고 y=1로 분류하려면 hΘ(x)는 대략 1이어야 하고, Θ^T는 0보다 커야 한다. y=0으로 분류하려면 hΘ(x)는 대략 0이고, Θ^T는 0보다 작다. 이때 1로 분류하는 비용함수를 Cost1, 0으로 분류하는 비용함수를 Cost0라고 하면, 로지스틱 회귀의 식은 왼쪽, SVM의 식은 오른쪽이 된다.
결론부터 말하자면 로지스틱 회귀와는 어디에 강조를 두느냐가 다르다. 아주 러프하게 표현하면,
로지스틱 회귀: A + λB
SVM: CA + B
가 된다. 비용함수에 방점을 두는가, 정규화에 방점을 두는가가 서로 다른 것이다. SVM의 기본 성질이 Large Margin, 즉 학습 데이터에 최적화fit되지 않게끔 하여 실제 데이터의 분류 정확도를 향상시키는 것이므로 어쩌면 당연한 말이다. C와 λ는 개념적으로 반비례 관계이다.
2-2. Fitting vs Regularization
로지스틱 회귀 문제에서는 A + λB를 작게 만드는 것이 목표였다. 람다가 커지면 정규화에 치중되어 람다B는 0에 가까워진다. 람다가 커지면 B안에 들어있는 세타들이 작아져서 high-order polynomial이었는데, 고차항들이 많이 사라진다. 차수가 올라갈수록 그래프 모양이 구불구불해졌던 것이니 차수가 내려가면 그래프가 스무스해진다. 람다에 무게를 너무 많이 주면 underfit이 될 수 있는 이유다. 즉, 람다B가 0에 가까워지게 만드는 최소화 문제로, 정규화항은 없어지는 것이나 마찬가지다. 이 과정에서는 A항만 남게 된다. SVM 문제에서는 CA + B를 작게 만드는 것이 목표로, C가 커지면 피팅에 치중(과적합 가능성 높음)되어 CA가 0에 가까워지고, CA가 0에 가까워지게 하는 최소화 문제가 되어 B항만 남게 된다. 결국 치중하고자 하는 부분의 반대 부분이 식에서는 남게 된다.
2-3. 가설

3. Large Margin Classifier
3-1. 결정 경계

비용함수의 계수 C가 아주 큰 수, 이를테면 10만 정도라고 가정하자. 그렇게 되면 y^(i)가 1일 때는 언제나 Θ^Tx^(i)는 1 이상이다. C가 어마어마하게 큰 수라면, 어쨌든 비용함수항을 최소로 만드는 것이 목적이므로 그에 곱해지는 수는 아주 작아지고, 결국 0에 가까워진다. 결과적으로는 min C*0의 형태로 볼 수 있는 것이다. 위 경우에서는 피팅 부분을 SVM이 무시할 수 있을 만큼 작게 만들었으므로 이렇게 되면 정규화항만 보게 된다.
3-2. 선형으로 나눌 수 있는 경우

위 직선들은 모두 훌륭하게 분류를 수행하고 있으나, SVM은 최적의 선을 찾는 기준을 'large margin'으로 본다. 즉, 분류할 값 각각에 대해 거리가 가장 큰 경우가 가장 좋은 직선이다. 위 경우에는 파란 실선이 그런 경우이다.
3-3. 이상치outlier가 있는 경우

동그라미만 있는 곳에 엑스가 하나 있다. 왼쪽 하단에 있는 X는 이상치이다. C가 아주 큰 경우라는 것은 정확도를 높이는(=더 잘 fit하게 하는) 것을 의미한다. 이전에 언급했듯이 정확하게 fit되는 것이 항상 좋은 것이 아니다. 이상치는 이상치로 두는 general한 분류기가 더 좋을 때가 많다. 위의 그림에서 빨간 선은 C가 아주 큰 경우이고, 검은 선은 C가 아주 크지 않은 경우이다. SVM은 large margin을 기준으로 분류기를 선택하므로, 검은 선을 더 좋다고 판단한다.
3-4. 수학적 접근: SVM 결정 경계
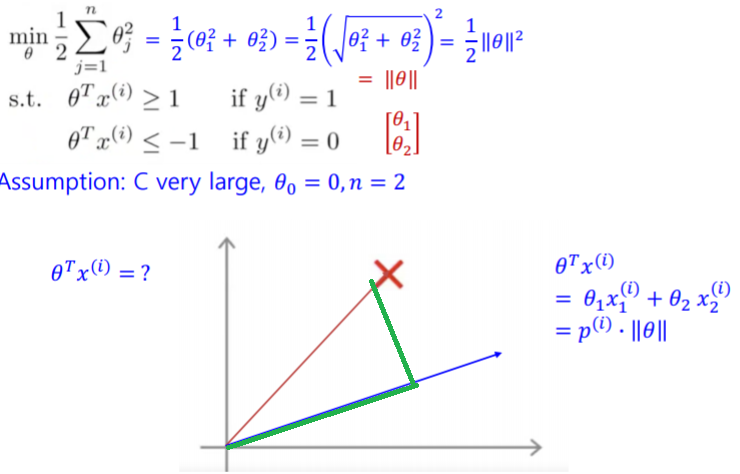
C가 아주 크다는 가정을 유지하고 식을 간단하게 하고자 Θ0=0 (원점을 지나는 그래프), n=2라고 둔다. 이에 근거하여 시그마 식을 전개하고, 루트 제곱 형태로 변형한다. 이는 결국 Θ의 길이의 제곱*1/2와 같다. 여기에서 결정 경계식을 그래프 상에 표현하는 것은 Θ^Tx^(i)=0를 그리는 것과 같다. 여기서 x^(i)를 기울기로 가지는 직선은 빨간 선이고, Θ^T를 기울기로 가지는 직선은 파란 선이다. x^(i)라는 벡터를 Θ에 프로젝션한 것을 p^(i)라고 부른다. 그림의 파란 선 위에 그려진 초록색 선 부분이다.
Θ^Tx^(i)는 두 개의 벡터 Θ^T와 x^(i)의 내적과 같은 말이다. 두 벡터의 내적을 E라고 치면, E가 가장 커지는 각도가 0도이고, E의 값이 0이 되는 각도는 90도이다. Θ^Tx^(i)=0을 표현하기 위해서는 벡터x^(i)의 모든 점은 벡터 Θ^T에 직교해야 한다.
* n = number of features
* m = number of samples
* Θ의 길이 = ||Θ|| = 놈/노름norm
* projection = 빨간 X에서 파란 선으로 직교하여 내려오는 것,
위 식을 선형대수에 근거해 약간 바꿔 쓰면 p^(i)*||Θ||가 된다.

우리가 찾고자 하는 것이 Θ의 값이라는 것을 항상 명심하자. 요약하면, SVM의 결정 경계는 가중치 벡터 Θ^T에 직교하면서 마진이 최대가 되는 직선을 찾는 것이다.

위와 같은 상황에서 결정 경계는 초록색 선, 가중치 벡터 Θ^T는 파란 선이다. 마진이 최대가 되는 직선이 좋은 직선이라고 하였으므로, 직관적으로 판단할 때 오른쪽이 훨씬 좋은 경우에 해당한다는 것을 알 수 있다. 왼쪽 그래프부터 살펴보면, 직교하는 Θ에 투영된 거리인 p가 너무 작다. p가 작다는 뜻은 ||Θ||가 아주 크다는 의미이므로 비용함수값이 커진다. (비용함수 = 1/2*||Θ||^2) 오른쪽 그래프를 보면 p가 크고, ||Θ||가 작아져 비용이 줄어들어 최적이 된다.
4. 커널 Kernels
4-1. 비선형 결정 경계

선형으로 분리할 수 없는 경우도 분명히 존재한다. 위 학습 데이터를 잘 분류할 복잡한 다항 피처를 생각해보면, Θ에 의해 가중된 전체 벡터의 합이 0 이상일 경우 1을 리턴, 아닐 경우 0을 리턴한다. 이를 다르게 표현하면 기존 X를 다양한 고차원 항으로 표현한 새로운 피처 f에 의해 곱해진 Θ의 합을 취하는 결정 경계를 계산하면 된다. 그러나 차수가 높은 x, 즉 f의 항 수가 엄청나게 늘어나면 이에 따라 결정 경계식도 굉장히 복잡해지고, 계산 시간이 오래 걸린다. 이런 경우 뭔가 다른 더 나은 방법이 '커널'을 사용해 주는 것이다.
4-2. 커널kernel
"유사도 함수: 주어진 데이터를 고차원 특징 공간으로 사상해주는 것"

저차원의 원래 공간에 커널 함수라는 매핑 함수를 사용하여 고차원에 매핑한다. 커널 함수는 유사도 함수인데, 유사도 구하는 방법이 많기 때문에 방법을 골라 쓰면 된다. 아무거나 커널로 쓸 수는 없고, 머서의 정리에 따른 특정 조건을 만족해야 사용 가능하다. 아래에서는 가우시안 커널을 사용한다. 이때 고차원 변환을 위한 계산 비용이 증가하여 차원이 아주 커질 경우에는 성능에 문제가 생긴다. 수학적으로 고차원 데이터를 내적하는 것과 내적한 결과를 고차원으로 보내는 것이 동일하다는 것을 이용한 커널 트릭을 사용한다. 즉 데이터를 고차원에 매핑하는 부분을 커널함수에 데이터를 넣는 부분으로 대체할 수 있다.

일단 3개의 피처를 정의하고, (x0는 0으로 무시) 이를 x1, x2 두 개의 차원에 표시한다. 그리고 2차원 공간에 3개의 임의의 점을 선택한다. 여기서 임의의 점을 랜드마크landmark 'l^(i)'이라고 한다. 새로운 x가 주어졌을 때, x와 l^(i)의 유사도를 f1으로 정의한다. 결국 페어와이즈로 전부 비교해가며 x가 l과 얼마나 '유사한지'를 계산한다. 이 계산 결과가 제곱으로 나와서 불편한데, 이를 벡터로 만든 것이 바로 f다. 계산을 편하게 만들기 위한 일종의 꼼수라고 볼 수 있겠다. 이 식을 풀어 쓴 공식에서 ||x-l^(i)||는 유클리디안 거리이고, 오메가는 표준편차, 오메가 제곱은 분산이다. 위 식은 f1=K(x, l^(i))로 정리할 수 있다. 이 공식에 커널 트릭을 적용한 것이 아래의 예이다.
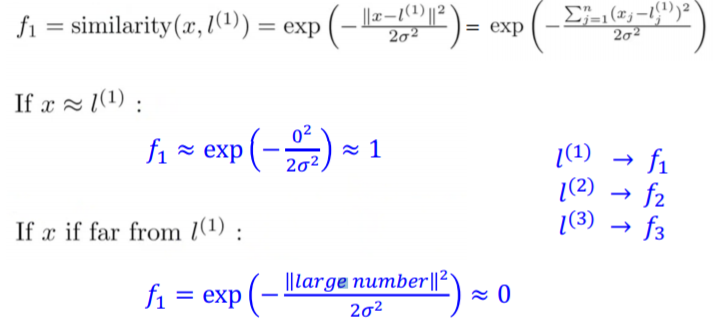
즉 거리가 아주 가까운 경우는 거리를 0으로 볼 수 있게 되어 f1을 1로 봐도 될 정도가 되고, 거리가 아주 먼 경우에는 분모가 아주 큰 수가 되는데, 아주 큰 음수에 대한 지수함수는 0에 수렴하므로 f1을 봐도 될 정도가 된다.
예시

커널함수와 f1의 관계를 그래프로 그려본 결과는 위와 같다. x가 랜드마크와 정확히 일치하면 f1=1이 된다. 랜드마크와 아주 떨어지면 f1=0에 가깝게 된다. 이렇게 x와 l이 얼마나 근접한지 계산할 수 있다. 이 그래프에서 분산이 하는 역할을 알아보기 위해 분산의 변화에 따른 기울기를 같이 표현했다. 분산이 0에 가까워질수록 기울기(경사)가 커지면서 폭이 좁아진다.
4-5. 가설 학습
위에서까지 정의된 조건을 이용하여 세우는 가설은 다음과 같다: 만약 학습 샘플 X가 Θ0 + Θ1f1 + Θ2f2 + Θ3f3 가 0 이상인 조건을 만족하면, 정답 1을 예측한다.
예시

이미 학습을 수행한 뒤, Θ값이 각각 Θ0=-0.5, Θ1=1, Θ2=1, Θ3=0으로 나왔다고 가정하자. 그러면 위와 같은 랜드마크를 가질 때, 새로운 샘플 X가 어떤 값을 예측할까? 먼저 붉은 점부터 살펴보면, 랜드마크 1번은 x와 아주 가깝고, 나머지는 멀다. 따라서 가설식은 -0.5 + 1*1 + 1*0 + 0*0으로, 0.5가 되고, 이는 0보다 크기 때문에 1을 예측한다. 하늘색 점도 같은 방식으로 살펴보면, 랜드마크 전부와 멀리 떨어져 있기 때문에 -0.5 + 1*0 + 1*0 + 0*0 = -0.5로, 0 미만이 되어 0을 예측하게 된다. 이러한 방식으로 비선형 경계를 분류할 수 있다.
4-6. Landmark 고르기

그렇다면 랜드마크는 어떻게 얻거나 고를 수 있는가? 일단 학습 데이터를 전부 읽어온다. 그리고 학습 데이터별로 랜드마크를 생성한다. 초기 랜드마크는 학습 데이터와 완전히 같은 위치에 있게 되는 것이다. 이후 새로운 샘플이 주어지면 모든 랜드마크와의 거리 f를 계산한다. 이때 Θ0는 bias이므로, 값을 유지한다.

이 계산 과정을 반복하면 자기 자신과 동일한 랜드마크와 비교하는 구간이 있다. 이 경우 가우시안 커널은 동일한 위치이므로 1로 평가한다. 이렇게 계산된 f값을 m+1 *1 차원의 벡터로 저장한다. 즉 f^(i)는 f 벡터의 i번째 데이터가 되는 셈이다.
4-7. SVM with kernels 결정된 f값을 SVM에서 활용하는 방법 (★)

이전에 Θ^T*f가 0 이상이면 y를 1로 분류한다고 말했다. 이때, f는 [m+1 * 1]의 벡터이다. Θ를 계산하는 방법은 SVM 최적화 알고리즘을 이용한다. 이 최적화 결과를 최소화하기 위해 f 벡터를 사용한다. 그리고 이 최적화 알고리즘을 계산하면 Θ를 찾을 수 있게 된다. 계산 성능 향상을 위해서는 위 식에서 m을 n으로 가정한다. 학습 데이터와 f벡터의 수가 같기 때문이다. 그리고 하단의 상자 안 공식에서 왼편(Θ^TΘ)을 구현하는 것보다 오른편(Θ^TMΘ)을 구현하는 것이 성능이 훨씬 좋다. 전부 유사도 계산을 하고 있기보다 덜 중요한 것을 빼주는 M을 넣어주는 것이다. 데이터가 많을 경우 수많은 for 루프를 돌리지 않고 행렬 연산을 하는 것도 방법이다.
5. SVM 사용하기
5-1. 파라미터들

SVM의 주요 파라미터는 C이다. 큰 C는 bias가 낮고 variance가 높은 경향을 보이며, 상대적으로 정규화 치중이 작다. 중앙의 수식은 가우시안 커널 함수이다. 커널 함수의 종류는 다양하지만 문제에 따라 최적의 커널 함수를 직접 학습하고 테스트하여 찾아야 한다. 이 예제에서는 가우시안 커널을 사용한다. 각 커널마다 최적화를 돕는 파라미터들이 따로 있다. 가우시안 커널의 경우에는 분모의 '시그마 제곱' 인데, 이 값이 크면 피처 f가 아주 스무스해진다. C가 작은 경우와 유사하다. C와 시그마제곱을 어떤 것으로 설정하는가에 따라 학습 결과가 달라진다.
가우시안 커널이 시그마제곱을 사용한다면, 이와 유사한 가우시안RBF의 파라미터는 1/2시그마제곱이다. 이를 감마라고 부른다. 시그마가 표준편차이므로, 감마가 클수록 시그마는 작다. 감마가 의미하는 것은 하나의 데이터 샘플이 영향력을 행사하는 거리이다. SVM을 plot으로 표현해보면 C가 동일할 때 감마가 커짐에 따라 경계가 구불구불해지는 것을 확인할 수 있다. 따라서 감마는 결정 경계의 곡률을 결정한다는 것을 알 수 있다.
5-2. Choices
파라미터 세타를 찾는 것은 liblinear나 libsvm과 같은 SVM 소프트웨어 패키지를 사용할 수 있다. 밝혀내야 할 것은 C와 kernel(유사도 함수)이다. 커널이 없는 경우도 있을 수 있다. 이 경우를 linear kernel이라고 부른다. liblinear가 이 경우 쓰는 패키지이다. 현장에서 사용하는 경우가 있다. column(차원) 수 n이 아주 큰데, 샘플 데이터 개수 m은 작을 때 사용한다. 커널을 쓰면 high order 식으로 overfit할 수 있기 때문이다.
가우시안 커널을 사용하기로 결정했다면, 시그마 제곱을 골라야 한다. 가우시안 커널은 n이 작거나 m이 클 때 사용한다. 둘 중 하나를 사용하면 좋겠지만, 둘 다 사용하기 싫다면 구현해도 된다. 어떤 패키지는 구현할 것을 요구한다.
5-3. 다른 kernels
다른 커널을 사용하는 것 자체는 문제가 없으나, 모든 유사도 함수가 유용한 것은 아니다. 위에서 짧게 언급했다시피 '머서의 정리'를 만족해야 한다. 그래야 최적화가 올바르게 진행되고, 발산diverge하지 않는다(=수렴converge한다). 가장 유명한 것은 리니어와 가우시안이고, 또 다른 커널에는 폴리노미알 커널, 스트링 커널, 카이스퀘어 커널 등이 있다.
6. 실습
6-1. XOR Prediction (sklearn)

간단한 문제라고 해서 항상 선형으로 분할되리라는 보장은 없다. 부울린 연산 and, or, not의 결과를 플라팅한 문제가 쉬운 예이다. 이는 선형 분리로는 불가능하지만, svm으로는 가능하다.
6-2. Iris.csv를 활용한 실습 (sklearn)
from sklearn import svm
…
clf = svm.SVC()
clf.fit(학습 데이터, 정답)
pre = clf.predict(테스트 데이터)
방법은 위처럼 간단한 편이다. 빌트인 커널과 커스텀 커널 모두를 쓸 수 있고, 가우시안 커널과 상당히 유사한 RBF, 리니어, 폴리노미알, 시그모이드가 빌트인으로 준비되어 있다. SVC()안에 파라미터로 gamma 값을 주면 RBF를, kernel='linear'를 쓰면 리니어 커널을 사용하게 된다.
7. 참고 자료
1. 명지대학교 전종훈 교수님 강의안
2. 벡터 연산에 대해 잘 설명한 블로그 (★)
4. 서포트 벡터 머신의 사용자로서 알아야 할 것들 (★)
5. 지수함수 위키피디아
'머신러닝' 카테고리의 다른 글
| 다중선형회귀 원리 (1) | 2019.06.04 |
|---|---|
| 텍스트마이닝 (0) | 2019.06.01 |
| [분류] 로지스틱 회귀 (0) | 2019.05.26 |
| k-fold 교차 검증 (0) | 2019.05.26 |
| 선형회귀 (0) | 2019.05.26 |




