Stack Building
다중선형회귀 원리 본문
1. 다중선형회귀Multi variable Linear Regression
1-1. 개념
특징값이 여러개로 표현된 입력 데이터에 대해 실수값을 출력하는 연속함수의 선형관계를 학습한다. 정답과 특징이 각각 하나씩일 경우에는 2차원 공간에 선형관계를 표현할 수 있으나, 특징이 2개 이상일 경우에는 다차원상에서 표현해야 한다.
1-2. 가설 표현

각 특징을 중심으로 정답 간의 관계를 2차원 평면으로 분리하면 서로 다른 기울기를 가진 직선으로 표현할 수 있다. 즉 다차원에서 표현되는 다중 선형 회귀는 각 특징을 표현하는 축의 기울기를 모두 구하여 결합해야 한다. 위의 그림에서 가격을 H, 아파트 평수를 X1, 전철역과 거리를 X2라고 둘 때, H = w1X1 + w2X2 + b 가 된다.

가설 검증 및 수정 과정은 기본적으로 선형 회귀와 같다. 먼저 예측 가설 값에서 실제 값을 뺀 총합의 평균으로 비용을 계산하고, 경사하강법을 적용하여 최소의 비용이 계산되도록 가설을 수정해 나간다. 이때 데이터를 구성하는 특징이 너무 많아지면 (예: 이미지 데이터) 식으로 표현하기 너무 길어진다. 이럴 경우, 행렬곱을 사용한다. 행렬 X에는 특징을, 행렬 W에는 기울기를 넣어 두면 행렬곱으로 다차원 직선을 식으로 쉽게 표현할 수 있게 된다.
2. 텐서플로우로 구현
2-1. 사용하는 함수
(1) 변수 정점
Variable()
- 자료 저장을 위한 정점을 구성
- () 안에 초기에 저장될 값을 전달할 수 있음
global_variables_initializer()
- 변수 정점에 초기화된 값을 세션에 전달
Variable()함수로 변수 정점을 만들고 초기화하는 과정
w = tf.Variable(tf.random_uniform([1], -100, 100))
…
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
(2) 난수 생성
random_uniform()
- 주어진 최소값과 최대값 사이의 정규분포 난수를 생성
random_uniform() 함수로 난수 생성 과정
n = tf.random_uniform([1], -100, 100)
1은 생성될 난수 개수, -100은 최소값, 100은 최대값
-100에서 100 사이의 숫자 하나를 임의로 만든다는 의미
(3) PlaceHolder 정점
placeholder()
- 세션이 실행된 후, 연결된 선분으로부터 전달받은 텐서를 차례로 전달받는 정점을 구성
- 세션이 실행될 때 해당 placeholder에 전달할 텐서를 지정 (feeding 과정)
placeholder() 함수로 place holder 정점을 만들고 텐서를 전달하는 과정
timeData = [1, 2, 3, 4, 5, 6, 7]
…
Time = tf.placeholder(tf.float32) #플레이스홀더 Time
…
sess = tf.Session()
sess.run(train, feed_dict={Time: timeData}) #텐서 전달
(4) 제곱, 평균, 경사 하강
square() : 전달받은 자료 제곱 연산
reduce_mean() : 전달받은 자료 평균 계산
GradientDescentOptimizer() : 설정된 하강률로 경사 하강을 수행하기 위한 객체 생성
경사 하강 객체의 minimize() : 최소 비용을 찾기 위한 경사 하강 수행
2-2. 선형 회귀
(1) 학습 과정
- 학습 데이터로 가설을 설정함
- 가설을 검증함
- 반복하여 가설을 조정함
- 회귀 모형 도출
(2) 텐서플로우 작업 과정
- 텐서플로우 명령어를 사용하여 그래프 구성
- 세션을 만들고 실제 데이터를 입력하여 그래프 실행
- 결과값을 바탕으로 그래프 업데이트
(3) 월급 예측 시스템의 그래프 구조

(4) 구현
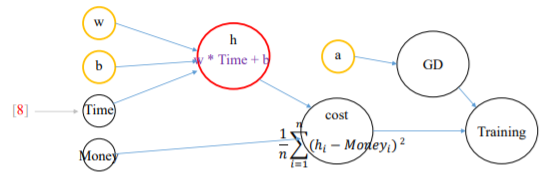
- 텐서플로우 사용 선언 및 객체 선언
import tensorflow as tf
- 학습을 위한 데이터 준비
timeData = [1, 2, 3, 4, 5, 6, 7]
moneyData = [25000, 55000, 75000, 110000, 128000, 155000, 180000]
- 그래프 구성
* 기본 입력값을 위한 노드 구성
(처음에는 임의의 숫자 지정, Time과 Money는 텐서값을 전달받을 플레이스 홀더. 텐서값이란 배열 원소를 말함.)
w = tf.Variable(tf.random_uniform([1], -100, 100))
b = tf.Variable(tf.random_uniform([1], -100, 100))
Time = tf.placeholder(tf.float32)
Money = tf.placeholder(tf.float32)
* 가설과 비용 계산식(예측 가설값에서 실제값을 뺀 것의 제곱의 합의 평균)정의
h = w * Time + b
cost = tf.reduce_mean(tf.square(h - Money))
- 그래프 구성: 경사하강법 선언
a = tf.Variable(0.01)
optimizer = tf.train.GradientDescentOptimizer(a)
train = optimizer.minimize(cost)
- 세션 실행: 세션을 만들고 텐서플로우 변수 초기화
* 텐서플로우는 값이 최초로 저장될 때나 변경될 때마다 변수를 초기화해야 변경값이 적용됨.
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
- 세션 실행: 가설을 반복 검증하며 w, b를 학습
for i in range(5001):
sess.run(train, feed_dict={Time: timeData, Money: moneyData})
if i % 500 == 0:
print(i, sess.run(w), sess.run(b))
- 학습된 선형 회귀 모형으로 수입 예측하기
print(sess.run(h, feed_dict={Time: [8]}))
2-3. 다중 선형 회귀
가설 검증, 수정 과정은 선형 회귀 방식과 같다.
(1) 기본적인 방법
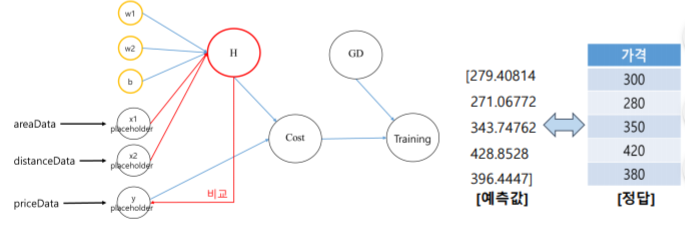
- 텐서플로우와 학습 데이터 준비
import tensorflow as tf
areaData = [20, 25, 25, 30, 32]
distanceData = [20, 100, 30, 20, 80]
priceData = [300, 280, 350, 420, 380]
- 학습 데이터 저장소(플레이스홀더) 준비
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
- 가설에 필요한 각 축의 기울기와 y절편 표현
w1 = tf.Variable(tf.random_normal([1]))
w2 = tf.Variable(tf.random_normal([1]))
b = tf.Variable(tf.random_normal([1]))
- 가설 설정과 비용 계산에 의한 가설 검증
h = x1 * w1 + x2 * w2 + b
cost = tf.reduce_mean(tf.square(h - y))
- 경사 하강법에 의한 가설 수정
optimizer = tf.train.GradientDescentOptimizer(0.00001)
train = optimizer.minimize(cost)
- 세션을 만들고 텐서플로우 변수 초기화
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
- 가설을 반복 검증하며 가중치와 절편을 학습
for i in range(5001):
sess.run(train, feed_dict={x1: areaData, x2: distanceData, y: priceData})
if i % 500 == 0:
print(i, sess.run(w1), sess.run(w2), sess.run(b))
- 정답과 비교하며 학습 모형 테스트
h_infer = sess.run(h, feed_dict={x1: areaData, x2: distanceData, y: priceData})
print(h_infer)
(2) 행렬곱을 사용하는 방법

2차원 배열은 따로 있지 않고 1차원 배열을 구성하는 각 공간에 또 다른 배열이 저장된 형식으로, 행렬 구조의 데이터를 표현하는 데에 효과적으로 사용할 수 있다.
- 텐서플로우와 학습 데이터 준비 (2차원 배열로 행렬구조로 자료 표현)
import tensorflow as tf
x_data = [[20., 20.],
[25., 100.],
[25., 30.],
[30., 20.],
[32., 80.]]
y_data = [[300.],
[280.],
[350.],
[420.],
[380.]]
- 학습 데이터 저장소 및 가설에 필요한 기울기와 y절편 준비
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([2, 1]))
b = tf.Variable(tf.random_normal([1]))
- 가설 설정과 비용 계산에 의한 가설 검증
hypothesis = tf.matmul(X, W) + b
cost = tf.reduce_mean(tf.square(hypothesis - Y))
- 경사 하강법에 의한 가설 수정
optimizer = tf.train.GradientDescentOptimizer(0.00001)
train = optimizer.minimize(cost)
- 세션을 만들고 텐서플로우 변수 초기화
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
- 세션 실행 – 가설을 반복 검증(2000번)하면서 w와 b를 학습
for i in range(5001):
sess.run(train, feed_dict={X: x_data,Y: y_data})
if i % 500 == 0:
print(i, sess.run(W), sess.run(b))
- 학습 모형 테스트
h_infer = sess.run(hypothesis, feed_dict={X: x_data})
print(h_infer)
3. 참고 자료
명지대학교 김제민 교수님 강의안
'머신러닝' 카테고리의 다른 글
| 클러스터링 (k-means 알고리즘) (0) | 2019.06.11 |
|---|---|
| 강화학습 (1) | 2019.06.04 |
| 텍스트마이닝 (0) | 2019.06.01 |
| [분류] SVM (0) | 2019.06.01 |
| [분류] 로지스틱 회귀 (0) | 2019.05.26 |




